



 |
 |
 |
 |
(Numerals in this document, where the context is ambiguous,
are dozenal unless otherwise stated by a preceding "d." for decimal.
"dd." is used, if necessary, as the dozenal prefix.)
Dear DSGB
Regarding dozenals and base twelve numeration... comments for or against... oh boy, where do I even begin?
This whole topic opens up a whole Pandora's box of limitless multitudes of related concepts worthy of intellectual consideration.
In the past, especially when I was living in the UK, I would from time to time hear some folks lament the loss of £sd, and how twelve makes a much better scale than ten due to its inherent divisibility (four factors vs. just two). Even my own father would occasionally mention it in passing, perhaps with a mild indifference, given the long standing state (and meek acceptance) of decimalization.
Every now and then, I would think to myself that a lot of scales that use twelve would fall little short of ideal for human mensuration purposes, if only it were not for the biologically motivated ten counting scale. And more recently, it occurred to me that there would likely be serious organizations promoting the development of base twelve instead of ten, and here we have the Dozenal Societies.
First off, the DSGB site is extremely neatly constructed and is embodied with meaningful and cogently written arguments, which is always a plus. Obviously, it is not complete as such, but it likely never will be, if only because there are so many avenues to explore in this fascinating subject.
The recently added page about the African dozenals is particularly interesting, especially since I am a little bit of a linguist myself. One does wonder if the Nimbian tribes ever did realize the potential of the twelve-adapted numbers they used, or if their main concern was simple counting, addition and subtraction, in and of themselves for which a decimal scale should prove equally serviceable.
(As a side note, it is hoped that these freshly imported pages you have added will have the numbers converted to Pitman numerals ASAP, instead of the ill thought out "A" and "B" symbols.) [Ed. I've changed them to T and E for the moment.]
Your fundamental premise of twelve being a superior base to ten is in my view perfectly sound. I also favour the use of Pitman's ten and eleven digits over the DSA suggestions, and especially over the uninspired hex derived "A" and "B" hacks.
However, in order even to begin convincing the general public of this fact, there are many points that will have to be qualified.
The most overwhelming hurdle that any advocate of any even provably and demonstrably superior system must face is social inertia (aka market forces). Unless some quasi-magical overwhelming benefit of universal or widespread conversion can be shown, it remains tragic but likely that the new system will remain a minority interest and will never gather sufficient ground even to come remotely close to a faint hope of displacing the old.
There are literally dozens (yes, dozens!) of examples of this that have occurred in the real world, and there are numerous reasons why humankind often develops a propensity toward adopting and subsequently retaining inferior systems. The keyboard on which I am currently typing is one very clear example. It has the keys arranged in the Dvorak layout, and while for many purposes this is a hugely superior set up to the more popular Sholes-Remington ("QWERTY") layout, it has remained relatively obscure throughout the duodecades since its inception.
The same, or similar principles, can be applied to base ten numeration (vs. base twelve), VHS cassettes (vs. the now obsolete BetaMax), DoT headlamps in North America (vs. the typically superior European specification beam pattern), just as a few obvious examples off the top of my head.
I might tentatively suggest that the only effective way to promote the widespread adoption of dozenal numerals worldwide is somehow to establish a situation whereby they may coexist with primitive decimals. The use of prefixes "d." for decimal and "dd." for duodecimal might be workable, but there would always remain the risk of confusion and the reluctance to adopt such "dual labelling".
Given the problems some folks had with the dual euro vs. old currency labelling on mainland Europe, I fear that the dozenal-decimal chasm would be even more difficult to bridge. But sensible and effective methods for permitting the coexistence of two common number bases without introducing a completely new set of numerals for base twelve need at least to be contemplated carefully. Your basic philosophy of avoiding the decimetric fanatics' tactic of trying to impose their will on the rest of us through force of law is to be lauded.
However, I cannot see that it would do the Society a great deal of harm to suggest new options and possibilities. My favoured idea for numerating up to a gross would be to retain the same names up to twelve/a dozen (if it ain't broke, don't fix it), followed by:
| 11 | onezen | 17 | sevenzen | |
| 12 | twozen | 18 | eightzen | |
| 13 | threezen | 19 | ninezen | |
| 14 | fourzen | 1T | tenzen | |
| 15 | fivezen | 1E | elevenzen | |
| 16 | sixen | 20 | two dozen |
This would follow the time honoured ten plus unit counting structure already in use for base ten numbers from d. 13 through 19. It is not beyond the realm of credibility that terms such as "zeenage" and even, Heaven forbid, "zeen 'zine" (!) would take root in similar fashion to their decimal counterparts. Surely even the least adept could understand this principle? (It also works rather beautifully in other Germanic languages, and it is easily possible for all of the counting traditions, e.g. the German reversal of the digit rôles for numbers over twenty, thirty etc. to be retained!)
The DSA refers to dd. 10 as "do", short for "dozen". While this may appear almost abhorrent to a select few, I have my suspicions that such an abbreviation would take root no matter what, so the numbers could well continue:
| 21 | two dozen and one / two do' one |
| 22 | two dozen and two / two do' two |
| 2E | two dozen and eleven / two do' eleven |
| 30 | three dozen / three do' |
| 40 | four do' |
| 50 | five do' |
| 60 | six do' |
| E0 | eleven do' |
| E1 | eleven do' one |
| EE | eleven do' eleven |
| 100 | gross |
| 101 | gross (and) one |
| 110 | gross (and) twelve/a dozen |
| 111 | gross (and) onezen |
| 200 | two gross |
| 300 | three gross |
| EEE | eleven gross eleven do' eleven |
| 1000 | liriad |
| 106 | miliad |
| etc. etc. |
All the above dozenal designations are clearly distinct from their decimal counterparts.
Now, onto the juicy stuff.
Myself, I have been "experimenting" with base twelve arithmetic just a wee little bit, especially where recurring prime fractions are concerned. I made various interesting observations, some of which are documented on your site, some of those of which I "discovered" before even having noticed that you had the same observations documented! Most notably that applies to the properties of periods of base twelve prime reciprocals, a most fascinating subject indeed.
One point I think you could address more clearly, since I consider it to be a major strength of base twelve, is the real world simplicity and useful representation of fractions. While you make the obvious point of dozenals greatly simplifying key basic fractions (especially thirds, vis-à-vis base ten) and critical primary universal relationships, I think you have thus far failed to place sufficient emphasis on the fact that these primary relationships and fractions already well represented, dozenals are logically vastly superior even when the dozenal fraction appears to be far more complex than its decimal equivalent!
Even I, someone very sympathetic to the dozenal idea, was amazed to discover this when I pondered over the old "What's the best way to carve up a birthday cake into five pieces?" problem. Consider this: of what use is the decimal 0·2 when attempting this feat? At first, decimals may appear much simpler and more logical for representing fifthsÉ but in fact by expressing the decimal 0·2, all we are really saying is that one fifth is equal to two tenths, which is of little consequence in the real world, since, as you aptly put it on your site, nature carries no preference for ten!
The decimal fraction, no matter how simple, is of little use if the entity we are dealing with is not easily represented in ten parts. Hence even the simple decimal fraction 0·2 is of little help with our quint-carving puzzle. Now, onto dozenals. The fraction 1/5 = dd. 0·24972497... at first appears to be absurdly long winded and complex in relation to its decimal counterpart. But wait! The repetend is still a manageable four digits in length, and for many everyday purposes this can easily be approximated to two duodecimal places with little issue: 1/5 = 0·25 (2 dd.p.)
Under a dozen base, the circle (birthday cake in our example) can easily be visualized in twelve segments, akin to the sectors defined by hour markings on the clock face - a straightforward representation for a small child to grasp.
And now, it is relatively easy to use our dozenal fractions to carve up the cake by noting the point just shy of halfway between two and three o'clock (but more than a third of the way theretwixt, since 0·24972497... > 0·24). The same idea is easily applied to the multiples of one fifth, 0·4972..., 0·7249... and 0·9724...
So the irony of ironies is that the decimal base can be proven inferior in working with fractions for which it ostensibly should take the podium and send twelve counting to the dustbin!
I took this idea a stage further.
Realizing the clear superiority of dozenals for these applications, or put another way that even complex dozenal fractions are far more useful and interesting than their decimal brethren in most cases, I experimented with other possible applications of prime fractions and circles with clock face divisions.
Remembering the fascination with the decimal number 142857, that base's first prime reciprocal cyclical reptend, and the "multigrams" or "enneagrams" associated therewith, I tried my hand at doing dozenal versions of these. Hey presto, with essentially nothing more than a pen and paper, I was drawing free hand enneagrams with dozenals. How wonderfully enchanting!
As you might imagine, given the esoteric obsession with d. 142857 enneagrams, I started with the dd. 186T35 enneagram, by connecting up one o'clock, eight o'clock, six o'clock, etc. right through five o'clock then back round to one o'clock again, which unsurprisingly comes out exactly the same, but is much easier to draw freehand due to the fraction being represented in a base that accepts fundamental real world useful divisors and relationships (in this instance laid out almost magically on the clock face around the circle).
Unable to resist the sheer temptation and fascination with these "discoveries", I was soon drawing away the ones for 2497 (butterfly), 076E45 (warped or "compressed" version of the 186T35 enneagram), 06316948421 (strangely lopsided due to the odd period), 0082336EE39885, 01599340ET62287E, 08579214E36429T7 (slightly weird and cluttered but not uninteresting), 008E53505280EE30686E693E (beautiful, this one!), 0478TT093598166E74311E28623T55, etc.
All the even period enneagrams are symmetrical about a half-past-eleven to half-past-five axis bisecting the centre of the circle, the digit zero representing twelve o'clock. Actually, the enneagram concept might make a neat side addition to your excellent pages dedicated to regular polygons, since the two are distantly related.
Along with this document, I have included text files outlining a small number of dozenal prime reciprocals and the periods of all dozenal primes up to 2EE.
My apologies if this is duplicating your most likely thorough library of existing resources on dozenal mathematics, but I sadly note that even mathematically devoted Internet sites make no space for their excellent and terrifyingly fascinating observations, in base twelve as opposed to just binary and/or decimal.
On the subject of dozenal divisibility tests, dozenal wins out easily for 3, 4 and 6, since these can easily be tested by direct observation, but otherwise it's a close call. Some advocate the adoption of base six because that base has simpler tests for 5 and 7 divisibility over E and dd. 11, but I think your polygon page goes some way toward refuting that.
Ultimately, divisibility tests aren't that critical in themselves, and in this particular regard, base twelve cannot easily be described as a clear winner, and indeed can be argued to have minor disadvantages over six, ten and sixty. Therefore that avenue is probably not the best one to take when making the (otherwise mostly very strong) case for twelve.
As for your comments on and apparent vociferous opposition to the imposition of the decimal (millimal even) metric system, your concerns are both well voiced and heard among the general public (even in already metric countries like this one to some degree), but again, I think the case against decimetric might be stronger were it better qualified.
Firstly, the decimal SI metric system is by no means all bad, since it imparts at least one obvious benefit: it establishes a standard set of tables that can define, and permit relatively simplified conversion between, all of the "weird and wonderful" non-standard customary units of various proportions and dispositions still in use around the world today.
Otherwise, when it comes to considering decimetric as a serious replacement for "human based" customary units, I totally agree with your view that this is not only undesirable, but also wholly unrealistic. "Tweaked" customary units continue to survive in rigidly metricated societies, which is actually no bad thing in itself.
With regards to the oft argued superiority of customary (Imperial or U.S.) measures, I must admit that I am in two minds about this. On the one hand, existing duodecimal scales such as ft. and in., and formerly s. and d., are clearly favourable given the dominance of a dozenal base for numeration.
Absent dozenal numbers, I must say that SI Metric does carry certain charms in comparison to Imperial, whose benefits cannot really be best realized without the use of a sensible and divisible number base. As for non-duodecimal Imperial units such as avoirdupois lb. and oz., I consider these utterly inferior in just about all respects, even compared to decimal metric, unless binary divisions are all that matter, all of a sudden. Along with the general retention of customary units such as ft. and in. and, most importantly, the common adoption of base twelve numeration, a push for duodecimalization of the entire system of Imperial measures can be seen to be desirable.
Tom Pendlebury's TGM proposal is a good example of what could be achieved, although I have my reservations and doubts over the viability of any metric that promises to supersede the seemingly inviolable second as the basic scientific unit of temporal mensuration and calculation.
The same goes for calendar reform: there are already twelve months in the year, and I personally believe that the benefits of merging the standard and astrological calendars would be marginal at best, almost certainly insufficient to cover the costs.
You have a page on dozenal music - very interesting, just like the rest of the site. This seems extremely logical, given the existing standard diatonic scale of twelve chromatic steps between "octaves". I experimented with thinking the dozenal way musically when listening to some of my favourite tunes (even if only in my head), but the truth be known, the "old" way is probably far too well established in my mind now to change systems (this is quite unlike converting to typing on the Dvorak keyboard, which I have done with reasonable success only quite recently).
Older studies also suggested that a musical scale set to a resolution of four do' five chromatic steps per "octave" would result in finer, nicer harmonies. This was actually attempted some time during the 11th grossury, though apparently to little tangible avail.
Worthy of note (no pun intended), though, is that in the standard twelve note scale, the 0 to 6 interval represents e.g. C to F# - not a very natural, simple or harmonious interval at all. Indeed this could be seen as a flaw in the system. The reason that the 0-6 interval does not generate a nice harmonious chord is likely associated with the logarithmic rather than linear chromatic increment vs. actual tonal frequency relationship.
If someone could perfect a 45-note scale based instrument, that would indeed be very interesting. Of course, it should not be too daunting to concoct an electronic or computerized equivalent in this day and age, with little more than simple audio editing software, a few logarithms and a little creativity!
With all the pro-dozenal reasoning to one side, let's look at the case against twelve.
In all fairness, a ten scale can serve us well if all we do with it is record integer values, count, add and subtract. Given that mathematics, more specifically, articulate numeracy, involves so much more that just that, there really is no case for ten on that front.
The Nimbians' mileage may vary. It is very easy to ask the question, "Given the clear general superiority of dozens, how have decimals managed to survive?", and this idea could be carried over to just about any inferior system in common use today, witness yet again the good old "QWERTY" keyboard that I'm not typing on, but many others continue to use.
I think this has been covered extensively elsewhere, perhaps by you, but one possible event that permits inferior systems, technologies, methodologies and ideologies to persist is marginalization. The inferior keyboard survives to this day partly by being marginalized by the now taken for granted yet indispensable mouse as the primary input device of choice. The decimal number system has survived by being marginalized, first by the ancient Sumerians, Babylonians and similar civilizations who used tens only to delineate the minor segments of their hybrid base sixty systems, then by more contemporary pre-Information Age societies who made (and continue to make) extensive use of non-decimal units and scales of mensuration, the most notable of which is of course the dozen.
And here and now in the Information Age into which we have all been wistfully whisked over the last few duodecades, the scale of ten has been swept aside by the scale of two, good old digital electronics, bistable circuits, binary logic and Boolean algebra. Many observers have suggested that it is this computerization and digitization that has rendered the perceived benefits of a better general human counting base to be effectively redundant. This is a hard (though by no means impossible) argument for a dedicated dozenalist to counter.
The decimalists will draw upon their advantage of societal inertia, that the decimal system is "already in common use" and that in this day and age of powerful binary computation devices, the case for total numerical upheaval through twelve conversion is minimal at best. And to a degree, these people would be quite right. But all is not lost for those who prefer reasoning and reckoning by the dozen. For starters, the prevalence of such competent and powerful computation devices makes just about all numerical operations (shy of certain specific needs such as factoring products of extremely large primes) pretty much trivial.
As such, we can all experiment in and work with different bases with relative ease. It is a matter for regret that there are few, if any, electronic calculators on the open market for sale at an agreeable price, that can reckon with the scale of twelve. I cannot help but notice your picture of a dozenal calculator complete with proprietary DSGB engraving. Is this electronic wonder a unique masterpiece? Did you get this machine specially made or do any manufacturers actually produce this equipment? If it is available, I would almost cut off an arm to get hold of one! [Ed.: sorry, this particular one I created with Photoshop... but we now have our own electronic version (Windows only so far)]
On balance then, there are several key aims that need to be achieved, long before universal dozenalization can be anything more than a (very) distant pipe dream:
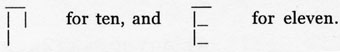
The case for twelve might be strengthened even further, even here and now in the Information Age, by politely suggesting to skeptics that it might not necessarily be in our long term best interests to become excessively dependent on electronics and computers, partly due to the relative inferiority, inefficiency and ineptitude of the number base still sadly in common use. Unfortunately, some might say that that trend is already well under way as we speak!
It goes without saying that I leave you free to do whatever you wish with this document and the side notes: read it, copy it, publish it, ignore it, ridicule it, trash it, it's your call.