



 |
 |
 |
 |
This problem concerns nodes and arcs.
One node |
Two nodes joined by 1 arc |
Three nodes joined by 3 arcs.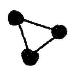 |
No, we aren't asking for the number of arcs required to join a given-number of nodes one to another; that's been asked often enough before. Four nodes are joined by 6 arcs. I can draw this result as
 or
or
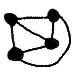
In the second diagram no arcs cross, while in the first we have produced an extra crossing-point.
So our first question is: for any given number of nodes, what is the minimum number of extra crossing-points we can have when each node is joined to every other;
and our second is: is there a formula connecting the number of nodes and the number of extra crossing-points?
I first suggested this topic to a class of 11 year olds - to be solved by trial and error.
By drawing, this class, and others, came up with :
| Nodes (x) | Extras (y) |
|---|---|
| 4 | 0 |
| 5 | 1 |
| 6 | 3 |
| 7 | 9 |
| 8 | 19 |
And it isn't too difficult to find a formula to fit these results:
y = 2(x - 5)2 + 1;
which is fine as long as the y-values above are the real minima.
From the formula we can then predict the minima for other x-values. For x = 9, for example, the y-value is 33. By actual drawing the least number obtained by any class was 36; and then on the last day of term one of the Lower Sixth achieved y = 33 by drawing.
Perhaps others would like to try this problem to confirm, or disprove, my conjecture that the formula is correct.
All comments and suggestions welcome!