



 |
 |
 |
 |
An appropriate unit of length is, of course, the basic requirement for any measuring system, so an anthropo-compatible range was an inevitable beginning. Names for components of this were transferred generically to comparable sizes as more definite means of determining these were found and simple relationships defined: some became more important than others, notably the Foot. There were two forms of this : the natural or ploughman's foot of twelve digits, about 9-1/2", which, in early days, was half the Egyptian natural cubit or forearm length of twenty four digits. This was used by the Celts and survives today in Wales and Scotland. The visual foot, towards which derivations by many methods have tended, is the more practicable by being the widest spacing that is comfortably perceived without head movement, and, therefore, the most efficient to use for a hand-held measuring tool.
Visual feet range from 13·2" for the Indus or Northern foot, described by Flinders Petric from a study of early buildings before an actual specimen was found, to 11·53 for the value of a Roman foot as used in southern England. The Romans took their foot from an early Greek unit of sixteen digits, 11·8", which they divided into twelve Pollices (thumbs) for incorporating into their uncia system of weights and measures. Larger, 14" feet, found in such diverse areas as Poland, Italy & China were probably half a Braccia or arm-length and favoured by cloth workers, an obvious measure for their purposes. William, of Maimesbury stated that our yard was a distance given by the outstretched arm of Henry I from nose to finger tips, which must have been the "Iron Ulna of our Lord the King" as given in mediæval documents. True or not, it was an appropriate way of fixing a length all could appreciate, forming now an Aunt Sally for intolerant metricists who can only mock at things they do not understand.
There is no definite evidence on the origin of the English foot, traces of which can be found in old buildings back to the tenth century. Both the Roman foot, with an 11·53 length, and the Greek common foot, 12·45", were used then in England for building work, so it has been suggested that our foot, which is known and used world-wide, was an average of the two; but units of length were not derived in this way. Many documents as far back as Saxon times give the length of a foot as duodecim uncias pollices (twelve thumb inches) and therein lies the clue: One legacy of the Roman occupation was a notion that XII thumbs made a foot, which was something any craftsman could do on the job in hand, without referring to an official measure if one existed, and would be sufficient today for non-critical work. It was thus a true anthropometric measure that Edward I legalised at three barley corns to its inch. Flinders Petrie deduced that our foot has remained unchanged within 1/2% since then, being based on principles acceptable to the users. I wonder how long the metre would survive without the aid of elaborate equipment and legal sanctions.
Of special interest is the Greek Olympic foot, 12·15" used for the lay-out of the Parthenon. This is a geodesic unit which divided a minute of arc on an assumed spherical Earth into 6000 parts, with 600 to a Stade for one tenth of a minute. This was remarkably close to our nautical mile, and of comparable accuracy to the original measurement for the metre, which is 0·2 mm shorter than was intended. The Egyptians estimated the minute as 5000 of their Remen units, so some authorities assume the Greeks obtained their Olympic foot from them, but the sexagesimal format indicates a Sumerian origin. Accurate measurements like these would be possible on extensive river flood plains, with angles obtained from sun shadows or star sightings.
Human-sized measures are essential to allow correct perspectives toward our daily affairs. Just as a valid unit of length complies with visual acuity, so weight, more correctly mass, is judged by our muscular reactions to it. Piles of cobbles found at Neolithic sites were evidently the camp arsenal, put ready to discourage prowling animals or repel unwanted visitors. These no doubt were selected for optimum range, accuracy and effect, with median weight somewhat less than a pound, appropriate for use by small stature people. The 'War Stones'. collected by Pitt-Rivers from Polynesian natives were heavier. It is not too extravagant to suggest that an acceptable modem unit of weight should be a direct descendant of early throwing weapons. Peaceful counterparts could be a tennis racket, 15-1/2 ounces, or the baseball bat, a two-handed 'weapon' of 32 oz. It would be interesting to conduct tests for the throwing theory: I suspect our Imperial pound, first designated as such under George IV, would prove to be on the light side, but the kilogramme far too heavy.
Cereal seeds, the units of settled living, by being readily available and appearing regularly in nearly the same sizes and weights, were widely used as reference standards for both. The Northern foot, in its area of origin, had ten divisions each containing five wheat grains end to end, but a final European form comprised twelve 'inches' of three fully grown barley cornes. Edward I, in 1305, specified three for his English inche without stating from which part of the car they should be taken (the middle florets of a cereal head open first so have a longer growing period). This omission is considered an evasion that allowed a retention of the larger Saxon foot and its yard, which were strongly held for land measurement; even the King had to be aware of this! Later documents state a large, medium and small corne, giving an average which is within 2% for modern seeds. So, five and a half new English yards became a legal value for the Rod, Pole or Perch of five Northern yards; a long stick used to control the ox team and measure the width of a cultivation strip - still that of an English vegetable allotment today.
In the Middle East, where cereals originated, weights were based on Shekels formed from 180 seeds of barley or wheat; stone weights have been found corresponding to binary divisions of them. Barley is a little heavier, and growing conditions vary, so a range of shekel weights is reported, but those from major centres are well authenticated. In Sumeria, the shekel was compounded by sexagesimal multiples (x 60s) for Minas and Talents, which maintained their values in that area for over 1500 years despite the coming, and going, of conquerors. The Mina is still represented by various Livres, Pfunds, Pfunts and Libras in Europe which were some 10% heavier than our Roman-based pound with for Phoenician shekels for its uncia. Edward III increased this to sixteen ounces to facilitate the wool trade with Florentine weavers. His pound weight, restored by Elizabeth I, survives today.
By comparison, the decimetric system comprises an awkward and socially inept combination of un-ergonomic units confined within an indivisible framework which disregards the essential requirements of a functional measurement system. It adapted nicely to the rising disciplines of Heat, Electricity and Mechanics dealing in concepts outside ordinary experience which use only arbitrary units linked by abstract calculations for their manipulation. It also suited the purposes of a rising bureaucracy found necessary to regulate the increasingly large quanitities of money, materials and men; which were becoming regarded in that order of importance. Just as the primitive counting scale of ten drifted into use for more advanced calculations before the implications of these were realised, so metric was devised prior to a full appreciation of the complete facilities that a truly scientific system of measure should provide.
Basic physical constants such as the velocity of light, or acceleration of Earth gravity, should at least be definable by whole numbers, which, almost perversely, metric just fails to do. A recommendation that 'g', 9·81 (m/s)/s in SI, be rounded up to ten, is positively dangerous because this is the base of the numerical system. The point-shifting facility, claimed to be a great advantage for decimalisation although all place-value numeration has this property, could easily be overlooked, or over-done, with serious consequences. A computer printout is often believed without question, and many a student will come to think that g =ten is a mere arithmetical ploy. In foot-pound-second dynamics the good approximation of 32 is a nice binary number that cancels out in many equations and its misplacement will not remain unnoticed.
The metre, at first intended to be one ten millionth of a meridian quadrant through Paris, was later defined by marks scribed on precious-metal bars whose distance apart could be read to one part in a million. But science and industry demanded even greater assurance, so in 1960 a metre length became officially 1,650,763·73 wavelengths of krypton 86 light, with an accuracy of four parts in a thousand million. Later, krypton light waves could be subdivided with the aid of helium-neon lasers, allowing a metre length to be measured to within the size of an atom! The techniques used also produced an internationally agreed value for the velocity of light, c, as 299,792,458·6 ±3 metres per second, assuming a length for the metre. The two standards had thus become interdependent, with uncertainties mutually transferable, and if one wore to be fixed the other could be specified with confidence. The metric cat had been chasing her tail in ever smaller circles that were reaching a limit beyond which it is needless, if possible, to go.
At a Conférence Générale des Poids et Mesures held in 1983 it was decided to accept the integral part of the above figure for c as an unquestioned value for the fundamental constant of the Universe, upon which its structure and our understanding of it depend. This allowed a final definition of the metre as "the length of path traversed by light in vacuum during an interval of 1/1299 792 458 of a second". This 'metre-second' is sometimes rounded down to 0·000 000 003 seconds, giving an impression of finality with elegance (ignoring the decimal incompatibility of the factor 3) but it should be followed by an indefinite number of figures, starting with 342... The problem of metrological integrality has not been evaded, and the use of rows of figures for a basic constant is still questionable.
Since time can now be measured more accurately than space - to 1 second in 300,000 years is claimed for the cæsium clock - it was inevitable that length would be defined by it, which the author of ref.7 admits is a bit bizarre. Measurements of frequency, the inverse of time, were required for the lasers used to calibrate wavelengths of the krypton standard emission. Hence, whilst there is some tangible connection back to the prototype metre, an ultimate assessment of its length is dependent on time. The situation is that length, determined as a function of time, is being equated to the velocity of light multiplied by time. The nature of time itself is still regarded as enigmatic by philosophers and physicists; Lewis Carroll has provided an apt description of its latest use whereby the body of the cat has faded into the background, leaving its grin suspended in mid-air.
In the manner of things scientific, this outcome would have resulted whatever arbitrary unit of length had been selected; even a human-compatible one. The only scientific aspects of the metre lie in the means with which it has been measured and refined. A compulsive quest to learn more and more about less and less ... has no effect on the day-to-day uses to which measurement is put; by far the major application, but regarded with disdain by those who have gained control of it.
Efforts are continually made to adapt metric for practical purposes, starting with Napoleon's Système Usuel ("metres? metres! Dites moi en tois!) for which small modifications to traditional French measures made them compatible with the new units - a third of a metre being its Pied, half a kilogramme the Livre and a litre the Pinte (the equivalent of our quart) complete with their essential dozenal and binary divisions. We now have the 30cm 'Metric foot' (incidentally the Geneva foot; pragmatic people the Swiss) of timber yard and D.I.Y. store with its twelve 25 mm 'inches' for thicknesses and bolt lengths to meet the need for utility and comprehension. These wait to have their binary divisions included to restore another advantage of our familiar ruler, an ability to find the mid-point of a spacing. A Russian scale in our collection has its centimetres divided into quarters, perhaps for this reason. Dispensing chemists measure out 30ml when asked for an ounce. Instrument scales and graph papers are divided into 2 mm spacings to avoid excessive accuracy or dense data. Ship's drafts are marked in two decimetric steps when not in feet, the metre being too coarse for bottom clearances except very large carriers; and separation for aircraft is still in feet.
Comments are frequently heard regarding the public misunderstanding of, and indifference to, scientific work; more serious is the aversion to it in schools. These are real concerns which largely result from science not being conducted in terms that are in accord with ordinary usage and experience. Further, as the traditional means whereby these are realised get withdrawn, even made illegal, people become increasingly alienated from their material environment. It could be that this process is purposeful, and technical rationalisation has acquired political undertones. The Establishment of any form of society almost instinctively recognises any trends that enhance its authority and control, not least by breaking contacts with the past so that we become more compliant in the future.
Many historical observers, from Cicero to Churchill, probably before, have stressed a need for continuity if a nation is to retain its identity. National measures, which have developed down the ages for convenience in use, form an important aspect of our cultural heritage besides determining attitudes to the physical world and our appreciation of it. These are now being steadily whittled away by many devious means, admittedly for commercial and administrative expediency. A full implementation of metric measures, with intended decimalised time and angle, will complete the triumph of counters over doers with benefits only to the former, leaving those who do the real work to ponder on how their thoughts and actions came to be so restrained.
We do recognise the need for an International system of measurement to conduct scientific work and discuss results, realising that decimetric methods have acquired squatters rights on this so far, largely supported by the bulk of technical applications that have adopted them. By being a system integrated with its numerical base, and so used for scientific purposes, metric is assumed to be founded on scientific principles, which is far from the case. Those who congratulate themselves on reaching the pinnacle of metrological excellence should realise that their material is flawed both in content and arrangement, inhibiting a proper understanding and definition of the material world such as is undertaken in scientific work and handicapping those who have to deal with it. John Quincy Adams, advising Congress on the metric question in 1821, wrote: "Decimal arithmetic is a contrivance of man for computing numbers, and is not a property of time, space or matter". Nature has no partiality for the number ten. True for all time.
Measurement should be made for man, not man for measurement. If the undoubted efforts expended developing the metric system had worked with more scientific and socially acceptable material, considered at the start, we would by now be employing sets of measures that were unifying links between all levels of use instead of barriers that metric alone often becomes.
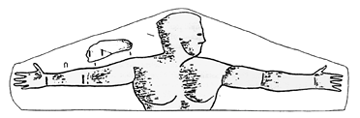
The illustration is of an Arundel Marble from the island of Paros, c.450 B.C.. showing the length standards of the day - the Fathom, Cubit, Fool, Span, Palm and Digit. The foot shown, 11·7 inches, is an early Greek unit of sixteen digits and the fathom of seven feet is considered to have been a reconciliation with four Egyptian royal cubits of 28 digits each. It is copied from the illustrations in references of Berriman and Connor, with additions by direct inspection of the bas relief sculpture, and reproduced here with permission of the Ashmolean Museum.
Values for the units mentioned vary slightly between authorities, but the principles invoked are not affected. Readers should judge these for themselves.