



 |
 |
 |
 |
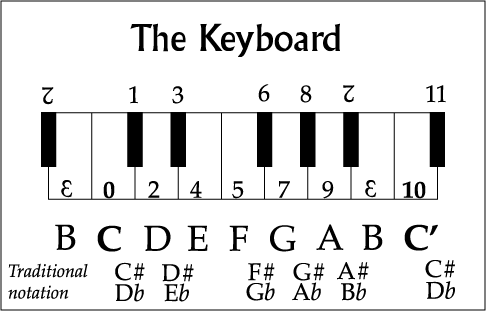
There are twelve equal semitones In an octave.
This has has been fundamentally true since the days of J. S. Bach, when a form of tuning musical instruments known as "Equal Temperament" was devised, but as can be seen above musicians
still refer to notes by the archaic idea of one scale of seven notes to the
octave, with sharps (meaning "another up" or +1) and flats ("another down" or -1)
to refer to the others.
The two white keys 0 and 10 (C and C') on the chart above are an "octave" apart.
(Counting up the white keys you have to count the top C as well as the bottom one to make it 8. This leads to bad arithmetic, for if you count up two octaves to the next C you will find that twice 8 is fifteen, not sixteen!! and 3 octaves make twenty two!!!)
If you play these two C notes together you will find that they sound almost like one single note. This is because the upper one does two vibrations for each vibration of the lower one.
An octave is a DOUBLE of frequency.
If a note is two octaves higher its frequency is (2 x 2 =) 4 times, and if three octaves (2 x 2 x 2 =) 8 times. Go n octaves up and the frequency is 2n times the lower note
A "semitone" is half a "tone", but the best definition of a tone is to say that It is two semitones! For a semitone is the step from one note on the keyboard to the next one up, e.g. from note 0 to note 1 is a semitone, from 3 to 4, 4 to 5 and so on.
As there are twelve of them to the octave a semitone is a ZENIDOUBLE of frequency. ("Zeni" prefix meaning "one dozenth of..." similar to "deci" for "one tenth of..."
In the traditional system the step from C to C sharp is called a "chromatic semitone" because both notes contain the letter C, but that from C to D flat (which Is identical in sound to C-sharp) is called a "diatonic semitone" because it goes up to the next letter of the alphabet!!
C-sharp and D-flat are called "enharmonics" - a word that means you change the names and manner of writing of the notes without changing their sound. In fact Note 8 is the only one in the scale that does not have three names, for there are also double sharps (+2) and double flats (-2). Then there are key signatures that contain so many sharps or flats according to which note you call "doh", and so it goes on and on.
More beginners have been put off learning music by this complicated rigmarole than by anything else.
Now look at the keyboard pattern at the beginning of this article and notice that C is the white key just left of a group of two black ones. Look at a piano and you find there are a lot of these Cs about.
Take hold of the jambs at the ends of the keyboard so that your arms are equally extended and the C you find most directly In front of your nose is called "Middle C". (It is the C nearest the lock if the piano has one and is marked in bold type on the chart).
Middle C is the note that musicians count up and down from. They speak of "the C below Middle C, or "the A flat below the double octave below Middle C" or "the F sharp in the third octave up from Middle C, etc.
In dozenal let us call Middle C "Note *60" (sixzen).
Then the C an octave above Middle C is note *70 (sevenzen) and the one an octave below Middle C Is Note *50 (fivezen), etc.
Every time you go up an octave you add one to the dozens figure, and every time you go down an octave take one off the dozens figure. We can now indicate any note directly by a simple number instead of the long-winded phrases used hitherto.
The G below Middle C becomes Note *57 (fivezen seven), A flat below the double octave below Middle C becomes Note *38 (threezen eight), and the F sharp In the third octave up from Middle C becomes Note *96.
Now to play a tune.
Find Middle C (Note *60), then counting upwards to the right and downwards to the left, play the following notes (count both black and white keys as in the keyboard table):
| 60 | 60 | 62 | 5E | 60 | 62 | ,64 | 64 | 65 | 64 | 62 | 60 | , | |||||||||||||
| 62 | 60 | 5E | 60 | ,67 | 67 | 67 | 67 | 65 | 64 | , | |||||||||||||||
| 65 | 65 | 65 | 65 | 64 | 62 | ,64 | 65 | 64 | 62 | 60 | 64 | 65 | 67 | , | |||||||||||
| 69 | 65 | 64 | 62 | 60 |
If you play it in the right rhythm, roughly indicated by the spacing of the numbers, you will play our national anthem. With a little practice you will get to know the pattern of the keyboard in respect to the units figures of the numbers.
Play the tune again but this time add 1 to each note number so that you play the next note up. It still sounds like "God Save the Queen" but a bit higher up. You have now "transposed" it from "the open key of C major" which has no sharps or flats Into the "remote key" of D flat which contains five flats in its "key signature", and at the same time even cleverer Into the "enharmonic equivalent" the "key of C sharp major" which contains seven in its "signature"!!!
Now find your Note 60 again and play up the white keys In order:
| 60 | 62 | 64 | 65 | 67 | 69 | 6E | 70 |
It sounds like Doh, ray, me, fah, soh, lah, te doh.
This Is known traditionally as the "scale of C major". Since the Note 0 sounds like the doh, let us call It the scale of 0-doh (pronounce: Oh-doh).
Play the scale again, this number. Again it sounds like doh, ray, me, etc (the same tune) but It is now Note 2 (62, 72, etc) that sounds like doh. This is the scale of "D Major" or 2-doh.
And so we go on for all the other scales: A flat Major is the scale or key of 8-doh, the scale of F-sharp major or G-flat major is the scale of 6-doh. After all, all that is meant by "the scale of G-flat major" is that your doh is G-flat, i.e. Note 6.
The explanation of how these major scales came about, with their steps of sometimes 2 zeniDoubles and some,times 1, will be given later.
All you have to remember to play a major scale is that it consists of three even numbers 0 2 4 then four odd ones 5 7 9 E and finally back to even at zen (10).
Just add to these your key number:
| doh | ray | me | fah | soh | lah | tee | doh | ||
| Basic | 0 | 2 | 4 | 5 | 7 | 9 | E | 10 | |
| For key 3-doh: +3 | 3 | 5 | 7 | 8 | T | 10 | 12 | 13 |
With a little practice you get to know that in 0-doh (the white keys) it is the Note 5 that sounds like fah, the Note E that sounds like tee, and so on. When playing in 3-doh, if the tune you are playing sounds In your mind as though it goes to fah, you play (5+3=) Note 8, for tee (E+3=) Note 12 and you get the right notes. Most mistakes by beginners when learning to play in keys other than C major are due to miscounting semitones caused by the queer way of counting by sharps and flats.
Now play another scale:
| 0 | 2 | 3 | 5 | 7 | 8 | E | 10 | |
| this sounds like | ||||||||
| lah | tee | doh | ray | me | fah | se | lah |
This sounds more solemn or serious than the bright major scale and is called the "minor scale". It sounds most like a finish when we stop at note lah, so we call this the scale of 0-lah (C minor).
For any other minor key add the note number of the keynote (lah); G minor is 7-lah, and by adding 4 or 7 respectively to the scale numbers you can play these scales without learning anything about sharps and flats:
The scale of 4-lah, add 4: 4 6 7 9 E 0 3 4
The scale of 7-lah, add 7: 7 9 T 0 2 3 6 7
When we added 4 to a scale or tune to shift it 4 zeniDoubles up, we were doing what in traditional language Is "transposing up by a major third".
Just as they counted octaves up the white keys and made life harder by counting both the top and bottom notes, so also with other "Intervals" (as they call differences), C D E was one two three-"a third"; also E F G was one two three "an Interval of a third".
In dozenal we see immediately that 7 (note G) minus 4 (note E) is 3 zeniDoubles, whereas 4 (note E) minus 0 (note C) is 4 zeniDoubles.
Finding that they had two different sorts of thirds they called one the "major third" (4 zeniDoubles) and the other the "minor third" (3 zeniDoubles).
They have all sorts of fancy names "perfect fifth", "diminished fifth", "augmented fifth" (7, 6 or 8 zeniDoubles resp.), and "enharmonic equivalents": "augmented second" and "minor third" both being 3 zeniDoubles, while a "diminished third is the same as a "maJor second".
Music teachers actually circumnavigate their own jargon by explaining that a minor third is one with 3 semitones, a major third one with 4.
Could anything be a better recommendation for the adoption of a system of numbering notes by semitones (zeniDoubles)?
All you have to learn about this in dozenal is that you Subtract one Note number from another to find the "interval" in zeniDoubles
. The Note differences are VERY IMPORTANT.
Melody is going up or down by the right amount from note to note, Harmony is being the right amount up or down from other notes played at the some time. So two notes together with their difference we call a SPAN, and speak of ONESPANS, TWOSPANS, THREESPANS, etc.
| Table of SPANS or "Intervals" | ||
|---|---|---|
| ZeniDoubles (semitones) | Dozenal name | Traditional names |
| 0 | Noughtspan, or Unison | Unison, Diminished second |
| 1 | Onespan | Semitone, Minor second |
| 2 | Twospan | Tone, Major second, Diminished third |
| 3 | Threespan | Minor third, Augmented second |
| 4 | Fourspan | Major third, Diminished fourth |
| 5 | Fivespan | Perfect fourth, Augmented third |
| 6 | Sixspan | Augmented fourth, Diminished fifth |
| 7 | Sevenspan | Perfect fifth, diminished sixth |
| 8 | Eightspan | Minor sixth, Augmented fifth |
| 9 | Ninespan | Major sixth, Diminished seventh |
| T | Tenspan | Minor seventh, Augmented sixth |
| E | Elvspan | Major seventh, diminished octave |
| 10 | Zenspan | Augmented seventh, Diminished ninth |
For three and four part harmony, full orchestra, etc., you play or sing three or more notes at the same time. These are called chords.
Play
| 67 64 60 | this is the chord of C Major |
now play:
| 67 63 60 | this is the chord of "C minor" |
Now add 7 to all of these numbers, and play the answers, and you have played the chords of "G major" and "G minor" resp.
To play a major chords select any note, count 4 zeniDoubles ups then another 3, making 7, and play the three notes arrived at. We can thus call a "major chord" a FOUR-SEVEN CHORD. 0 + 4 and 7 is the chord of C major", 7 + 4 and 7 i.e. Notes 7, E and 12 is the chord of "G major", etc.
The minor chord is a THREE-SEVEN CHORD, + 3 and 7.
| Table of CHORDS | ||
|---|---|---|
| Traditional names | Meaning in zeniDoubles | Dozenal name |
| Major chord, Major triad | + 4, 7 | A four-seven chord |
| Minor chord, Minor triad | + 3, 7 | A three-seven chord |
| Dominant seventh chord | + 4, 7, T | A four-seven-ten chord |
| Diminished seventh chord | + 3, 6, 9 | A three-six-nine chord |
| Augmented triad | + 4, 8 | A four-eight chord |
| Dominant major ninth chord | + 4, 7, T, 12 | A 4-7-T-2 chord |
(NB In the more complex chords some of the lower notes get omitted as in the
last example.
ZeniDouble notation makes the structure quite clear without ambiguity.)
| Dominant minor ninth chord | + 4, 7, T, 11 | A 4-7-T-1 chord |
| Dominant eleventh chord | + 7, T, 15 | A 7-T-5 chord |
| Dominant minor thirteenth chord | + 4, T, 18 | A 4-T-8 chord |
| Dominant major thirteenth chord | + 4, T, 19 | A 4-T-9 chord |
| Chord of the added sixth (major) | + 4, 7, 9 | A 4-7-9 chord |
| Chord of the added sixth (minor) | + 3, 7, 9 | A 3-7-9 chord |
| Neapolitan sixth | + 3, 8 | A three-eight chord |
| Italian sixth | + 4, T | A four-ten chord |
| French sixth | + 4, 6, T | A four-six-ten chord |
| German sixth | + 4, 7, T | A four-seven-ten chord |
To understand how to use them is, of course, another story, but all you have to do to hear what they sound like with no follow-up is to play the notes as shown by the numbers.
Most Instruments and voices have a bottom note and a top note below and above which they cannot go. The range of notes they can play or sing is called their COMPASS. A full compass piano usually runs from Note 29 to Note T0 and piano-makers could express that as a compass 29-T0. It is obvious from this (T0 - 29 = 73) that it comprises seven and a quarter octaves.
The compass of a song can be quoted on the front cover by a simple pair of dozenal numbers, e.g. 62-7T. The soprano singer about to purchase it and knowing that her vital statistics cantabile are 60-79 would ask if the shop held another copy in a lower key - that is as long as the accompaniment is written in a form not easily transposed. With a change of notation dozenal can probably solve this also.
The strings of a violin are tuned to the Notes 57, 62, 69, 74 (all at intervals of 7 zeniDoubles), and those of the 'cello to 40, 47, 52, 59; add zen (10) to those of the 'cello and you have the strings of the viola.
When two instruments or singers are performing out of tune there is a difference of frequency much less than one zeniDouble between them.
To get the best quality performance it is essential that instruments are made to give exactly the same number of vibrations for the same note. There is an internationally agreed standard that Note 69 (A above Middle C) vibrates at 440(dec) cycles per second.
An instrument, tuned to this, gives for Note 78, *100·2536 vibrations per quedriHour (hour divided by the fourth power of the dozen), and Note 68, *100·2536 vibrations per queniDay (day divided by the fifth power of Zen).
So the dozenal standard for Musical Pitch is:
Note 78 (A-flat about an octave and a half above Middle C) = *100 c/4Hr
which is the same as:
Note 68 (A-flat above Middle C) - *100 cycles/ 5Day
Instruments tuned to this and playing with others tuned to the international pitch are so close that only professional tuners can tell the difference and only then when high notes are played slowly.
is another aspect of music that spurns tens counting and falls right into the dozenist's lap. We will look at this in a later article.